Find the equation of the line use exact numbers – In the realm of mathematics, the equation of a line holds immense significance, serving as a cornerstone for understanding and analyzing linear relationships. This comprehensive guide delves into the intricacies of finding the equation of a line using exact numbers, empowering readers with the knowledge to unravel the mysteries of linear equations.
By harnessing the precision of exact numbers, we can uncover the slope and y-intercept of a line, enabling us to precisely describe its path through the coordinate plane. Moreover, the equation of a line provides a powerful tool for making predictions, solving problems, and gaining insights into real-world phenomena governed by linear relationships.
1. Identifying the Equation of a Line
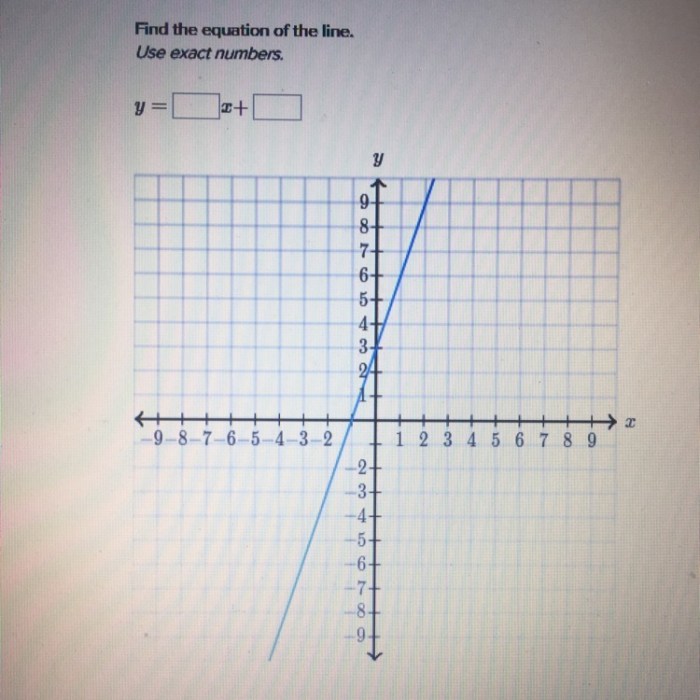
The equation of a line is a mathematical expression that describes the relationship between the coordinates of points on the line. It can be written in different forms, including slope-intercept form, point-slope form, and two-point form.
The slope of a line is a measure of its steepness, and it is calculated by dividing the change in y-coordinates by the change in x-coordinates between two points on the line. The y-intercept of a line is the value of y when x is 0.
The equation of a line can be used to graph the line and to make predictions about the coordinates of points on the line.
2. Using Exact Numbers to Find the Equation of a Line: Find The Equation Of The Line Use Exact Numbers
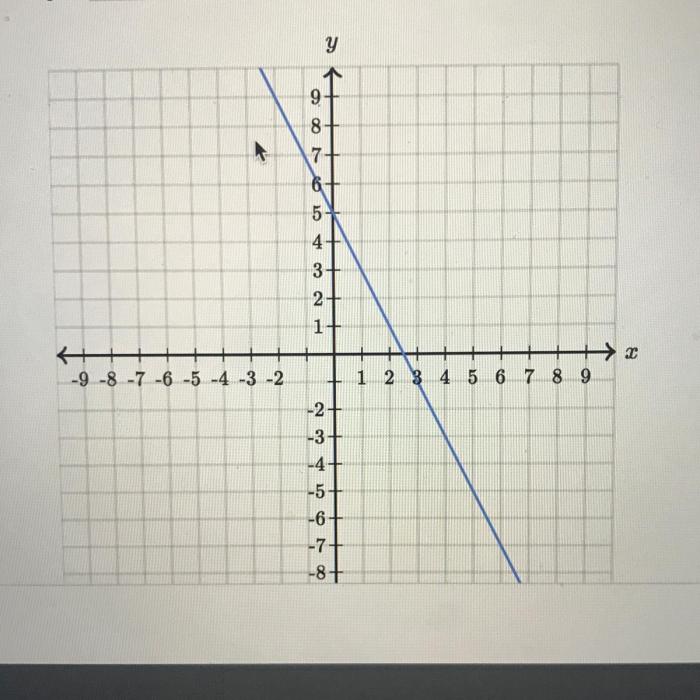
When using exact numbers to find the equation of a line, the slope of the line can be calculated by dividing the difference between the y-coordinates of two points on the line by the difference between the x-coordinates of the same two points.
Once the slope of the line has been calculated, the y-intercept can be found by substituting the coordinates of one of the points on the line into the slope-intercept form of the equation of a line and solving for b.
Using exact numbers to find the equation of a line ensures that the equation is accurate and that it can be used to make precise predictions about the coordinates of points on the line.
3. Applications of the Equation of a Line
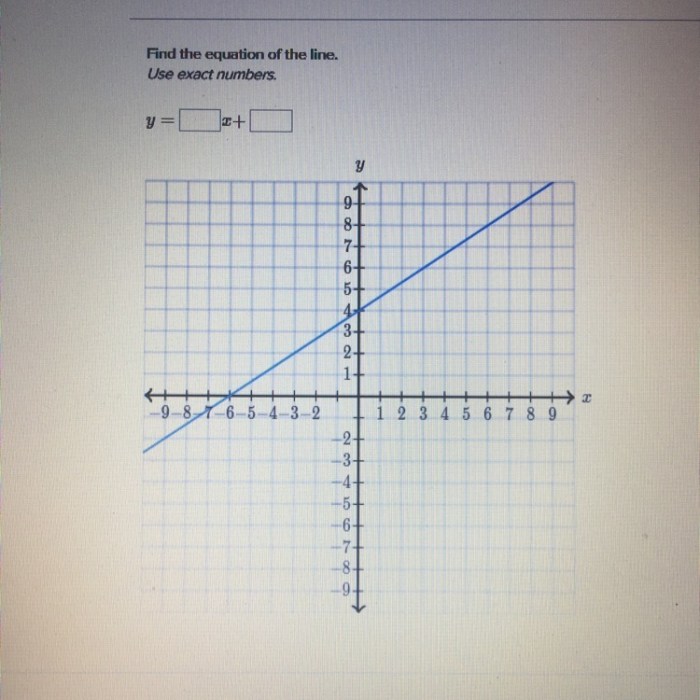
The equation of a line has many applications in various fields, including physics, economics, and engineering.
In physics, the equation of a line can be used to describe the motion of an object. For example, the equation of a line can be used to calculate the velocity of an object if its position is known at two different times.
In economics, the equation of a line can be used to describe the relationship between the price of a good and the quantity of the good that is demanded. For example, the equation of a line can be used to predict the price of a good if the quantity of the good that is demanded is known.
In engineering, the equation of a line can be used to design structures. For example, the equation of a line can be used to calculate the load that a beam can support.
4. Advanced Topics in Linear Equations
In addition to the basic concepts of the equation of a line, there are also more advanced topics that can be explored.
One advanced topic is the concept of parametric equations of lines. Parametric equations are a way of representing a line using two equations, one for the x-coordinate and one for the y-coordinate.
Parametric equations are often used to represent lines that are not parallel to either the x-axis or the y-axis.
Detailed FAQs
What is the slope of a line?
The slope of a line measures its steepness and is calculated as the ratio of the change in y to the change in x.
How can I find the equation of a line given two points?
To find the equation of a line given two points, use the point-slope form: y – y1 = m(x – x1), where m is the slope and (x1, y1) is one of the given points.
What are the limitations of using the equation of a line?
The equation of a line assumes a linear relationship between two variables. It may not accurately represent relationships that are nonlinear or have exceptions.
